本文共 11512 字,大约阅读时间需要 38 分钟。
12.1 什么是高可用性
总的来说,应用在超过一定的点以后追求更高的可能性是非常困难的,成本也会很高,因此我们建议设定一个更现实的目标并且避免过度设计。幸运的是,建立2个9或3个9的可用时间的目标可能并不困难,具体情况取决于应用。
有时候人们将可用性定义成服务正在运行的时间段。我们认为可用性的定义还应该包括应用是否能以足够好的性能处理请求。有许多方法可以让一个服务保持运行,但服务并不是真正可用。对一个很大的服务器而言,重启MySQL之后,可能需要几个小时才能充分预热以保证查询请求的响应时间是可以接受的,即使服务器只接收了正常流量的一小部分也是如此。 另一个需要考虑的问题是,即使应用并没有停止服务,但是否可能丢失了数据。如果服务器遭遇灾难性故障,可能多少都会丢失一些数据,例如最近已经写入(最新丢失的)二进制日志但尚未传递到备库的中继日志中的事务。你能够容忍吗?大多数应用能够容忍;因为替代方案大多非常昂贵且复杂,或者有一些性能开销。例如,可以使用同步复制,或者将二进制日志放到一个通过DRBD进行复制的设备上,这样就算服务器完全失效也不用担心丢失数据。(但是整个数据中心也有可能会掉电)。 一个良好的应用架构通常可以降低可用性方面的需求,至少对部分系统而言是这样的,良好的架构也更容易做到高可用。将应用中重要和不重要的部分进行分离可以节约不少工作量和金钱,因为对于一个更小的系统改进可用性会更容易。12.2 导致宕机的原因
我们首先对宕机事件按表现方式而非导致的原因进行分类。一般来说,“运行环境”是排名第一的宕机类别,大约35%的事件属于这一类。运行环境可以看作是支持数据库服务器运行的系统和资源集合,包括操作系统、硬盘以及网络等。性能问题紧随其后,也是约占35% ,然后是复制,占20% ,最后剩下的10%包含各种类型的数据丢失或损坏,以及其他问题。
我们对事件按类型进行分类后,确定了导致这些事件的原因。以下是一些需要注意的地方: • 在运行环境的问题中,最普遍的问题是磁盘空间耗尽。 • 在性能问题中,最普遍的宕机原因确实是运行很糟糕的SQL,但也不一定都是这个原因,比如也有很多问题是由于服务器Bug或错误的行为导致的。 • 糟糕的Schema和索引设计是第二大影响性能的问题。 • 复制问题通常由于主备数据不一致导致。 • 数据丢失问题通常由于DROP TABLE的误操作导致,并总是伴随着缺少可用备份的问题。 复制虽然常被人们用来改善可用时间,但却也可能导致宕机。这主要是由于不正确的使用导致的,即便如此,它也阐明了一个普遍的情况:许多高可用性策略可能会产生反作用,我们会在后面讨论这个话题。 现在我们已经知道了主要宕机类别,以及有什么需要注意,下面我们将专门介绍如何获得高可用性。12.3 如何实现高可用性
可以通过同时进行以下两步来获得高可用性。首先,可以尝试避免导致宕机的原因来减少宕机时间。许多问题其实很容易避免,例如通过适当的配置、监控,以及规范或安全保障措施来避免人为错误。第二,尽量保证在发生宕机时能够快速恢复。最常见的策略是在系统中制造冗余,并且具备故障转移能力。这两个维度的高可用性可以通过两个相关的度量来确定:平均失效时间(MTBF)和平均恢复时间(MTTR)。一些组织会非常仔细地追踪这些度量值。
第二步,通过冗余快速恢复,这里是最应该注意的地方。12.3.1 提升平均失效时间(MTBF)
以下是从我们的白皮书中摘录的指导性建议,在白皮书中有我们详细的分析结果。
• 测试恢复工具和流程,包括从备份中恢复数据。 • 遵从最小权限原则。 • 保持系统干净、整洁。 • 使用好的命名和组织约定来避免产生混乱,例如服务器是用于开发还是用于生产环境。 •'谨慎安排升级数据库服务器。 • 在升级前,使用诸如Percona Toolkit中的pt-upgrade之类的工具仔细检査系统。 • 使用InnoDB并进行适当的配置,确保InnoDB是默认存储引擎。如果存储引擎被禁止,服务器就无法启动。 • 确认基本的服务器配置是正确的。 • 通过 skip_name_ resolve 禁止 DNS • 除非能证明有效,否则禁用査询缓存。 • 避免使用复杂的特性,例如复制过滤和触发器,除非确实需要。 • 监控重要的组件和功能,特别是像磁盘空间和RAID卷状态这样的关键项目,但也要避免误报,只有当确实发生问题时才发送告警。 • 尽量记录服务器的状态和性能指数,如果可能就尽量久地保存。 • 定期检査复制完整性。 • 将备库设置为只读,不要让复制自动启动。(这一点很重要,只有确定复制发生的问题后,才重新启动复制) • 定期进行査询语句审査。 • 归档并清理不需要的数据。 • 为文件系统保留一些空间。在GNU/Linux中,可以使用-m选项来为文件系统本身保留空间。还可以在LVM卷组中留下一些空闲空间。或者,更简单的方法,仅仅创建一个巨大的空文件,在文件系统快满时,直接将其删除。 • 养成习惯,评估和管理系统的改变、状态以及性能信息。12.3.2 降低平均恢复时间(MTTR)
使用集群系统和冗余结构。这些是有用的,但要记住这些系统依然会失效。
12.4 避免单点失效
找到并消除系统中的可能失效的单点,并结合切换到备用组件的机制,这是一种通过减少恢复时间(MTTR)来改善可用性的方法。
可以采用两种方法来为系统增加冗余:增加空余容量和重复组件。增加容量余量通常很简单一一可以使用本章或前一章讨论的任何技术。一个提升可用性的方法是创建一个集群或服务器池,并使用负载均衡解决方案。如果一台服务器失效,其他服务器可以接管它的负载。有些人有意识地不使用组件的全部能力,这样可以保留一些“动态余量”来处理因为负载增加或组件失效导致的性能问题。出于很多方面的考虑会需要冗余组件,并在主要组件失效时能有一个备件来随时替换。冗余组件可以是空闲的网卡、路由器或者硬盘驱动器——任何能想到的可能失效的东西。完全冗余MySQL服务器可能有点困难,因为一个服务器在没有数据时毫无用处。这意味着你必须确保备用服务器能够获得主服务器上的数据。共享或复制存储是一个比较流行的办法,但这真的是一个高可用性架构吗?让我们深入其中看看。
12.4.1共享存储或磁盘复制
共享存储能够为数据库服务器和存储解耦合,通常使用的是SAN。使用共享存储时,服务器能够正常挂载文件系统并进行操作。如果服务器挂了,备用服务器可以挂载相同的文件系统,执行需要的恢复操作,并在失效服务器的数据上启动MySQL.这个过程在逻辑上跟修复那台故障的服务器没什么两样,不过更快速,因为备用服务器已经启动,随时可以运行。当开始故障转移时,检査文件系统、恢复InnoDB以及预热是最有可能遇到延迟的地方,但检测失效本身在许多设置中也会花费很长时间。
共享存储有两个优点:可以避免除存储外的其他任何组件失效所引起的数据丢失,并为非存储组件建立冗余提供可能。因此它有助于减少系统一些部分的可用性需求,这样就可以集中精力关注一小部分组件来获得高可用性。不过,共享存储本身仍是可能失效的单点。
共享存储本身也有风险,如果MySQL崩溃等故障导致数据文件损坏,可能会导致备用服务器无法恢复。我们强烈建议在使用共享存储策略时选择InnoDB存储引擎或其他稳定的ACID存储引擎。一次崩溃几乎肯定会损坏MyISAM表,需要花费很长时间来修复,并且会丢失数据。我们也强烈建议使用日志文件系统。使用非日志型文件系统和SAN(这是文件系统的问题,跟SAN无关)导致数据损坏无法恢复。
磁盘复制技术是另外一个获得跟SAN类似效果的方法。MySQL中最普遍使用的磁盘复制技术是DRBD(http://www.drbd.org),并结合Linux-HA项目中的工具使用。 事实上可以调整DRDB的同步级别,将其设置成异步等待远程设备接收数据,或者在远程设备将数据写入磁盘前一直阻塞住。同样,强烈建议为DRBD专门使用一块网卡。DRBD是一个以Linux内核模块方式实现的块级别同步复制技术。它通过网卡将主服务器的每个块复制到另外一个服务器的块设备上(备用设备),并在主设备提交块之前记录下来。由于在备用DRBD设备上的写入必须要在主设备上的写入完成之前,因此备用设备的性能至少要和主设备一样,否则就会限制主设备的写入性能。同样,如果正在使用DRBD磁盘复制技术以保证在主设备失效时有一个可随时替换的备用设备,备用服务器的硬件应该跟主服务器的相匹配。带电池写缓存的RAID控制器对DRBD而言几乎是必需的,因为在没有这样的控制器时性能可能会很差。
如果主服务器失效,可以把备用设备提升为主设备。因为DRBD是在磁盘块层进行复制,而文件系统也可能会不一致。这意味着最好是使用日志型文件系统来做快速恢复。一旦设备恢复完成,MySQL还需要运行自身的恢复。原故障服务器恢复后,会与新的主设备进行同步,并假定自身角色为备用设备。 从如何实际地实现故障转移的角度来看,DRBD和SAN很相似:有一个热备机器,开始提供服务时会使用和故障机器相同的数据。最大的不同是,DRBD是复制存储——不是共享存储——所以当使用DRBD时,获得的是一份复制的数据,而SAN则是使用与故障机器同一物理设备上的相同数据副本。换句话说,磁盘复制技术的数据是冗余的,所以存储和数据本身都不会存在单点失效问题。这两种情况下,当启动备用机器时,MySQL服务器的缓存都是空的。相比之下,备库的缓存至少是部分预热的。 DRBD有一些很好的特性和功能,可以防止集群软件普遍会遇到的一些问题。一个典型的例子是“脑裂综合征”,在两个节点同时提升自己为主服务器时会发生这种问题。可以通过配置DRBD来防止这种事件发生。但是DRBD也不是一个能满足所有需求的完美解决方案。我们来看看它有哪些缺点:- DRBD的故障转移无法做到秒级以内。它通常至少需要几秒钟时间来将备用设备提升为主设备,这还不包括任何必要的文件系统恢复和MySQL恢复。
- 它很昂贵,因为必须在主动-被动模式下运行。热备服务器的复制设备因为处于被动模式,无法用于其他任务。当然这是不是缺点取决于看问题的角度。
- 对于MyISAM表实际上用处不大,因为MyISAM表崩溃后需要花费很长时间检查和修复。对任何期望获得高可用性的系统而言,MyISAM都不是一个好选择;请使用InnoDB或其他支持快速、安全恢复的存储引擎来代替MyISAM。
- DRBD无法代替备份。如果磁盘由于蓄意的破坏、误操作、Bug或其他硬件故障导致数据损坏,DRBD将无济于事。此时复制的数据只是被损坏数据的完美副本。你需要使用备份(或MySQL延迟复制)来避免这些问题。
- 对写操作而言增加了负担。具体会增加多少负担呢?通常可以使用百分比来表示,但这并不是一个好的度量方法。你需要理解写入时增加的延迟主要由网络往返开销和远程服务器存储导致,特别是对于小的写入而言延迟会更大。尽管增加的延迟可能也就0.3ms,这看起来比在本地磁盘上I/O的4 ~ 10ms的延迟要小很多,但却是正常的带有写缓存的RAID控制器的延迟的3~4倍:使用DRBD导致服务器变慢最常见的原因是MySQL使用InnoDB并采取了完全持久化模式,这会导致许多小的写入和fsync()调用,通过DRBD同步时会非常慢。 我们倾向于只使用DRBD复制存放二进制日志的设备。如果主动节点失效,可以在被动节点上开启一个日志服务器,然后对失效主库的所有备库应用这些二进制日志。接下来可以选择其中一个备库提升为主库,以代替失效的系统。 说到底,共享存储和磁盘复制与其说是高可用性(低宕机时间)解决方案,不如说是一种保证数据安全的方法。只要拥有数据,就可以从故障中恢复,并且比无法恢复的情况的MTTR更低。{即使是很长的恢复时间也比不能恢复要快。)但是相比于备用服务器启动并一直运行的架构,大多数共享存储或磁盘复制架构会增加MTTR。有两种启用备用设备并运行的方法:我们在第10章讨论的标准的MySQL复制,以及接下来会讨论的同步复制。
12.4.2 MySQL同步复制
当使用同步复制时,主库上的事务只有在至少一个备库上提交后才能认为其执行完成。这实现了两个目标:当服务器崩溃时没有提交的事务会丢失,并且至少有一个备库拥有实时的数据副本。大多数同步复制架构运行在主动-主动模式。这意味着每个服务器在任何时候都是故障转移的候选者,这使得通过冗余获得高可用性更加容易。
- MySQL Cluster MySQL中的同步复制首先出现在MySQL Cluster (NDB Cluster)ₒ它在所有节点上进行同步的主-主复制。这意味着可以在任何节点上写入.这些节点拥有等同的读写能力。毎一行都是冗余存储的,这样即使丢失了一个节点,也不会丢失数据,并且集群仍然能提供服务。尽管MySQL Cluster还不是适用于所有应用的完美解决方案,但正如我们在前一章提到的,在最近的版本中它做了非常快速的改进,现在已经拥有大量的新特性和功能:非索引数据的磁盘存储、增加数据节点能够在线扩展、使用ndbinfo表来管理集群、配置和管理集群的脚本、多线程操作、下推(push-down)的关联操作(现在称为自适应査询本地化}、能够处理BLOB列和很多列的表、集中式的用户管理,以及通过像memcached协议一样的NDb API来实现NoSQL访问。在下一个版本中将包含最终一致运行模式,包括为跨数据中心的主动-主动复制提供事务冲突检测和跨WAN解决方案。简而言之,MySQL Cluster是一项引人注目的技术。现在至少有两个为简化集群部署和管理提供附加产品的供应商:Oracle针对MySQL Cluster 的服务支持包含了 MySQL Cluster Manager I具)Severalnines 提供了 Cluster Control I(http://www.severalnines.com),该工具还能够帮助部署和管理复制集群。
- Perc on a XtraDB Cluster Percona XtraDB Cluster 有许多优点: • 提供了基于InnoDB的透明集群,所以无须转换到另外的技术,例如NDB这样完全不同的技术需要很多学习成本和管理。 • 提供了真正的高可用性,所有节点等效,并在任何时候提供读写服务。相比较而言,MySQL内建的异步复制和半同步复制必须要有一个主库,并且不能保证数据被复制到备库,也无法保证备库数据是最新的并能够随时提升为主库。 •节点失效时保证数据不丢失。实际上,由于所有的节点都拥有全部数据,因此可以丢失任意一个节点而不会丢失数据(即使集群出现脑裂并停止工作)。这和NDB不同,NDB通过节点组进行分区,当在一个节点组中的所有服务器失效时就可能丢失数据。 • 备库不会延迟,因为在事务提交前,写入集合已经在集群的所有节点上传播并被确认了。 •因为是使用基于行的日志事件在备库上进行更新,所以执行写入集合比直接执行更新的开销要小很多,就和使用基于行的复制差不多。
当结合多线程应用的写入集合时,当然我们也需要提及Percona XtraDB Cluster的一些缺点:
• 它很新,因此还没有足够的经验来证明其优点和缺点,也缺乏合适的使用案例。 • 整个集群的写入速度由最差的节点决定。因此所有的节点最好拥有相同的硬件配置,如果一个节点慢下来(例如,RAID卡做了一次battery-learn循环),所有的节点都会慢下来。如果一个节点接收写入操作变慢的可能性为P,那么有3个节点的集群变慢的可能性为3P₀ • 没有NDB那样节省空间,因为每个节点都需要保存全部数据,而不是仅仅一部分。但另一方面,它基于Percona XtraDB (innoDB的增强版本),也就没有NDB关于磁盘数据限制的担忧。 • 当前不支持一些在异步复制中可以做的操作,例如在备库上离线修改schema,然后将其提升为主库,然后在其他节点上重复离线修改操作。当前可替代的选择是使用诸如Percona Toolkit中的在线schema修改工具。不过滚动式schema升级(rolling schema upgrade)在写作本书时也即将发布。 • 当向集群中增加一个新节点时,需要复制所有的数据,还需要跟上不断进行的写入操作,所以一个拥有大量写入的大型集群很难进行扩容。这实际上限制了集群的数据大小。我们无法确定具体的数据。但悲观地估计可能低至100GB或更小,也可能会大得多。这一点需要时间和经验来证明。 • 复制协议在写入时对网络波动比较敏感,这可能导致节点停止并从集群中踢出。所以我们推荐使用高性能网络,另外还需要很好的冗余。如果没有可靠的网络,可能会导致需要频繁地将节点加入到集群中。这需要重新同步数据。在写本书时,有一 个几乎接近可用的特性,即通过增量状态传输来避免完全复制数据集,因此未来这并不是一个问题。还可以配置Galera以容忍更大的网络延迟(以延迟故障检测为代价),另外更加可靠的算法也计划在未来的版本中实现。 • 如果没有仔细关注,集群可能会增长得太大,以至于无法重启失效节点,就像在一个合理的时间范围内,如果在日常工作中没有定期做恢复演练,备份也会变得太过庞大而无法用于恢复。我们需要更多的实践经验来了解它事实上是如何工作的。 •由于在事务提交时需要进行跨节点通信,写入会更慢,随着集群中增加的节点越来越多,死锁和回滚也会更加频繁。(参阅前一章了解为什么会发生这种情况。) Percona XtraDB Cluster和Galera都处于其生命周期的早期,正在被快速地修改和改进。在写作本书时,正在进行或即将进行的改进包括群体行为、安全性、同步性、内存管理、状态转移等。未来还可以为离线节点执行诸如滚动式schema变更的操作。12.4.3基于复制的冗余
复制管理器通常监控和管理三件事:应用和MySQL间的通信、MySQL服务器的健康度,以及MySQL服务器间的复制关系。它们既可以修改负载均衡的配置,也可以在必要的时候转移虚拟IP地址以使应用连接到合适的服务器上,还能够在一个伪集群中操纵复制以选择一个服务器作为写入节点。大体上操作并不复杂:只需要确定写入不会发送到一个还没有准备好提供写服务的服务器上,并保证当需要提升一台备库为主库时记录下正确的复制坐标。
这听起来在理论上是可行的,但我们的经验表明实际上并不总是能有效工作。 一个比较新一点的工具是Yoshinori Matsunobu的MHA工具集(http://code.google.com/p/mysql-master-ha/)。它和MMM一样是一组脚本,使用相同的通用技术来建立一个伪集群,但它不是一个完全的替换者;它不会去做太多的事情,并且依赖于Pacemaker来转移虚拟IP地址。一个主要的不同是,MHA有一个很好的测试集。 基于复制的冗余最终来说好坏参半。只有在可用性的重要性远比一致性或数据零丢失保证更重要时才推荐使用。问题是许多用户不知道如何去证明自己有资格并评估复制“轮盘赌”是否适合他们。这有两个方面的原因。第一,他们并没有看到“玻璃天花板”,错误地认为一组虚拟IP地址、复制以及管理脚本能够实现真正的高可用性。第二,他们低估了技术的复杂度,因此也低估了严重故障发生后从中恢复的难度。一些人认为他们能够使用基于复制的冗余技术,但随后他们可能会更希望选择一个有更强保障的简单系统。
其他一些类似的复制,例如DRBD或者SAN,也有它们的缺点。
12.5故障转移和故障恢复
冗余是很好的技术,但实际上只有在遇到故障需要恢复时才会用到。冗余一点儿也不会增加可用性或减少宕机。在故障转移的过程中,高可用性是建立在冗余的基础上。当有一个组件失效,但存在冗余时,可以停止使用发生故障的组件,而使用冗余备件。冗余和故障转移结合可以帮助更快地恢复,如你所知,MTTR的减少将降低宕机时间并改善可用性。
故障转移的缘由各部相同。我们已经讨论了其中的一些,因为负载均衡和故障转移在很多方面很相似,它们之间的分界线比较模糊。总的来说,我们认为一个完全的故障转移解决方案至少能够监控并自动替换组件。它对应用应该是透明的。负载均衡不需要提供这些功能。 故障转移最重要的部分就是故障恢复。如果服务器间不能自如切换,故障转移就是一个死胡同,只能是延缓宕机时间而已。在一些应用中,故障转移和故障恢复需要尽量快速并具备原子性。12.5.1 提升备库或切换角色
提升一台备库为主库,或者在一个主-主复制结构中调换主动和被动角色,这些都是许多MySQL故障转移策略很重要的一部分。具体细节参见第10章。
12.5.2 虚拟IP地址或IP接管
可以为需要提供特定服务的MySQL实例指定一个逻辑IP地址。当MySQL实例失效时,可以将IP地址转移到另一台MySQL服务器上。这和我们在前一章提到的思想本质上是相同的,唯一的不同是现在是用于故障转移,而不是负载均衡。
这种方法的好处是对应用透明。它会中断已有的连接,但不要求修改配置。有时候还可以原子地转移IP地址,保证所有的应用在同一时间看到这一变更。当服务器在可用和不可用状态间“摇摆”时,这一点尤其重要。 以下是它的一些不足之处: •需要把所有的IP地址定义在同一网段,或者使用网络桥接。 •改变IP地址需要系统root权限。 •有时候还需要更新ARP缓存。有些网络设备可能会把ARP信息保存太久,以致无法即时将一个IP地址切换到另一个MAC地址上。我们看到过很多网络设备或其他组件不配合切换的例子,结果系统的许多部分可能无法确定IP地址到底在哪里。 •需要确定网络硬件支持快速IP接管。有些硬件需要克隆MAC地址后才能工作。 •有些服务器即使完全丧失功能也会保持持有IP地址,所以可能需要从物理上关闭或断开网络连接。这就是为人所熟知的“击中其他节点的头部”(shoot the other node in the head,简称STONITH).它还有一个更加微妙并且比较官方的名字:击剑 (fencing).
12.5.3中间件解决方案
可以使用代理、端口转发、网络地址转换(NAT)或者硬件负载均衡来实现故障转移和故障恢复。这些都是很好的解决方案,不像其他方法可能会引入一些不确定性(所有系统组件认同哪一个是主库吗?它能够及时并原子地更改吗?),它们是控制应用和服务器间连接的中枢。但是,它们自身也引入了单点失效,需要准备冗余来避免这个问题。
使用这样的解决方案,你可以将一个远程数据中心设置成看起来好像和应用在同一个网络里。这样就可以使用诸如浮动IP地址这样的技术让应用和一个完全不同的数据中心开始通信。你可以配置每个数据中心的每台应用服务器,通过它自己的中间件连接,将流量路由到活跃数据中心的机器上。图12-1描述了这种配置。
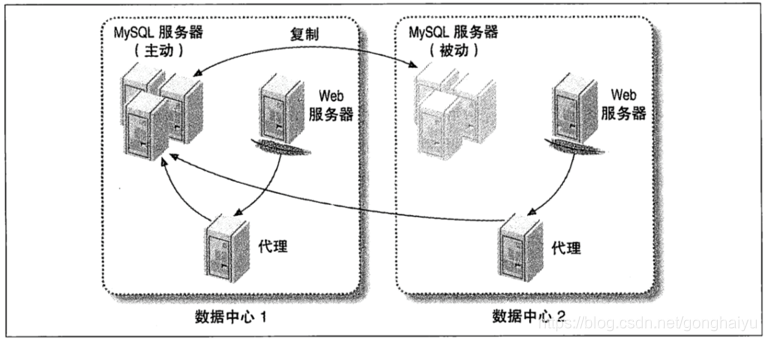 图12-1:使用中间件来在各数据中心间路由MySQL连接
图12-1:使用中间件来在各数据中心间路由MySQL连接 如果活跃数据中心安装的MySQL彻底崩溃了,中间件可以路由流量到另外一个数据中心的服务器池中,应用无须知道这个变化。
这种配置方法的主要缺点是在一个数据中心的Apache服务器和另外一个数据中心的MySQL服务器之间的延迟比较大。为了缓和这个问题,可以把Web服务器设置为重定向模式。这样通信都会被重定向到放置活跃MySQL服务器的数据中心。还可以使用HTTP代理来实现这一目标。图12-1显示了如何使用代理来连接MySQL服务器,也可以将这个方法和许多别的中间件架构结合在一起,例如LVS和硬件负载均衡器。
12.5.4在应用中处理故障转移
可以通过减少宕机来获得高可用性,这需要从以下两个方面来思考:增加两次故障之间的正常运行时间(MTBF),或者减少从故障中恢复的时间(MTTR)。
有时候让应用来处理故障转移会更简单或者更加灵活。例如,如果应用遇到一个错误,这个错误外部观察者正常情况下是无法察觉的,例如关于数据库损坏的错误日志信息,那么应用可以自己来处理故障转移过程。虽然把故障转移处理过程整合到应用中看起来比较吸引人,但可能没有想象中那么有效。大多数应用有许多组件,例如任务、配置文件,以及用不同语言编写的脚本。将故障转移整合到应用中可能导致应用变得太过笨拙,尤其是当应用增大并变得更加复杂时。但是将监控构建到应用中是一个好主意,当需要时,能够立刻开始故障转移过程。应用应该也能够管理用户体验,例如提供降级功能,并显示给用户合适的信息。12.6总结
可以通过减少宕机来获得高可用性,这需要从以下两个方面来思考:增加两次故障之间的正常运行时间(MTBF),或者减少从故障中恢复的时间(M盯R)。
另外一个减少恢复时间的策略是为系统建立冗余,并使系统具备故障转移能力,这样当故障发生时,可以在冗余组件间进行切换。不幸的是,冗余会让系统变得相当复杂。现在应用不再是集中化的,而是分布式的,这意味着协调、同步、CAP定理、拜占庭将军问题,以及所有其他各种杂乱的东西。这也是像NDB Cluster这样的系统很难创建并且很难提供足够的通用性来为所有的工作负载提供服务的原因。但这种情况正在改善,也许到本书第四版的时候我们就可以称赞一个或多个集群数据库了。 本章和前面两章提及的话题常常被放在一起讨论:复制、可扩展性,以及高可用性。我们已经尽量将它们独立开来,因为这有助于理清这些话题的不同之处。那么这三章有哪些关联之处呢? 在其应用增长时,人们一般希望从他们的数据库中知道三件事: • 他们希望能够增加容量来处理新增的负载而不会损失性能。 • 他们希望保证不丢失已提交的事务。 •他们希望应用能一直在线并处理事务,这样他们就能够一直赚钱。 为了达到这些目的,人们常常首先增加冗余。结合故障转移机制,通过最小化MTTR来提供高可用性。这些冗余还提供了空闲容量,可以为更多的负载提供服务。 当然,除了必要的资源外,还必须要有一份数据副本。这有助于在损失服务器时避免丢失数据,从而增强持久性。生成数据副本的唯一办法是通过某种方法进行复制。不幸的是,数据副本可能会引入不一致。处理这个问题需要在节点间协调和通信。这给系统带来了额外的负担,这也是系统或多或少存在扩展性问题的原因。数据副本还需要更多的资源(例如更多的硬盘驱动器,更多的RAM),这会增加开销。有一个办法可以减少资源消耗和维护一致性的开销,就是为数据分区(分片)并将每个分片分发到特定的系统中。这可以减少需要复制的重复数据的次数,并从资源冗余中分离数据冗余。
所以,尽管一件事总会导致另外一件事,但我们是在讨论一组相关的观点和实践来达成一系列目的。他们不仅仅是讲述同一件事的不同方式。 最后,需要选择一个对你和应用有意义的策略。决定选择一个完全的端到端(end-to-end)高可用性策略并不能通过简单的经验法则来处理,但我们给出的一些粗略的指引也许会有所帮助。 为了获得很短的宕机时间,需要冗余服务器能够及时地接管应用的工作负载。它们必须在线并一直执行査询,而不仅仅是备用,因此它们是“预热”过的,处于随时可用的状态。如果需要很强的可用性保证,就需要诸如MySQL Cluster, Percona XtraDB Cluster,或者Clustrix这样的集群产品。如果能容忍在故障转移过程中稍微慢一些,标准的MySQL复制也是个很好的选择。要谨慎使用自动化故障转移机制,如果没有按照正确的方式工作,它们可能会破坏数据。 如果不是很在意故障转移花费的时间,但希望避免数据丢失,就需要一些强力保证数据的冗余——例如,同步复制。在存储层,这可以通过廉价的DRBD来实现,或者使用两个昂贵的SAN来进行同步复制。也可以选择在数据库层复制数据,可以使用的技术包括 MySQL Cluster, Percona XtraDB Cluster 或者 Clustrix„ 也可以使用一些中间件,例如Tungsten Replicator.如果不需要强有力的保护,并且希望尽量保证简单,那么正常的异步复制或半同步复制在开销合理时可能是很好的选择。转载地址:http://cmurz.baihongyu.com/